Aplicación de los mapas de Karnaugh

    La aplicación de los mapas de Karnaugh tiene  lugar en el diseño de circuitos automatizados.    

Esta herramienta permite simplificar ecuaciones sin utilizar el análisis de simplificación de ecuaciones del álgebra  de Boole.

·        A partir de la tabla de verdad se coloca en las casillas de estados el valor lógico de salida (unos o ceros).

·        Luego se agrupan los estados verdaderos (unos) para obtener la ecuación simplificada.

Veamos un ejemplo, se desea que.

·        Una mesa transportadora sea movida por botones pulsadores mientras estos estén activados y limitada su carrera por interruptores de limite.

Mesa transportadora de mando por pulsadores

1.- Es importante determinar  todos los estados en  la tabla de la verdad para después trasladarlo al mapa de Karnaugh.

Tabla de la verdad

El problema es de lógica combinatoria, es decir no es necesario seguir una secuencia predeterminada de funcionamiento, podemos elegir mover a la izquierda o derecha o del estado 2 regresar al uno. Para cada condición de entrada existe solo un valor de  salida, para cada una de las 2 variables de salida.

En nuestro diseño no existe la posibilidad de funcionamiento que se active los dos limites de carrera al mismo tiempo.

También es importante que determinemos que si se presionan ambos pulsadores, se ordene el paro de la mesa, esta condición debe verse reflejada en nuestro Mapa de Karnaugh.

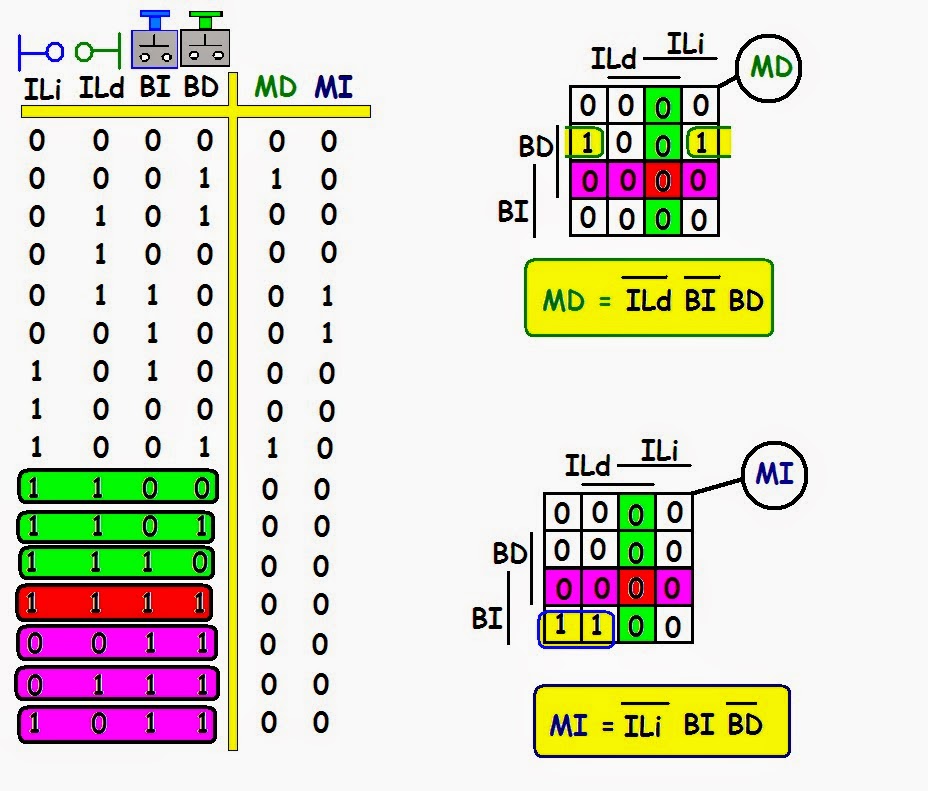
Solución con Mapas de Karnaugh

·        Es importante señalar que al encontrar la ecuación  se eliminan la(s) variable(s) que cambian de valor.

.- Para MD; ILi toma valores de cero y uno por lo que no va en la ecuación, las que no varían ILd negada y BD y BI negada.

.- Para MI; ILd es la que cambia por lo que no aparece en la ecuación. 

Circuito Eléctrico de mesa transportadora

Mapas de Karnaugh

Un mapa de Karnaugh es la parte principal de un método gráfico para la simplificación de ecuaciones lógicas.

En estos mapas se colocan todos los valores binarios (1 ó 0) de estados de una salida de  una tabla de verdad, en las celdas que representan los estados de las variables de entrada.  

Mapa de Karnaugh de 2 variables, tamaño y color

Estas celdas tienen una representación  bidireccional y son ordenadas siguiendo el código Gray, de manera que solo una variable de entrada de las variables varia entre celdas  adyacentes.

Mapa de Karnaugh permite localizar grupos

Los Mapas de karnaugh nos permiten relacionar grupos  y la idea es obtener el menor número de grupos. 

Mapa de Karnaugh  nos permite localizar grupos

Como ejemplo  veamos el siguiente problema.

Ejemplo de método de Mapa de Karnaugh

Como cada grupo conserva las variables que no cambian, en nuestro ejemplo la variable “B”  como cambia se elimina el resultado es S = A.

Circuitos lógicos equivalentes

El más simple es el mejor y fue obtenido utilizando Mapa de Karnaugh

Aplicación del Álgebra Booleana

Su aplicación es la de simplificar ecuaciones lógicas, para obtener circuitos equivalentes mas pequeños (simples) base de las instalaciones y máquinas automatizadas.

El Álgebra Booleana es utilizada  en el diseño de circuitos de conmutación  lógicos y para describir el  funcionamiento de  estos circuitos. 

Ejemplo: Diseño de circuito lógico para "Mesa transportadora" 

Planteamiento.

El inicio es el  planteamiento de un proceso o maquina automatizada. El que queremos y con que elementos.

 Por ejemplo, queremos que se mueva una mesa de trabajo hacia la derecha o a la  izquierda ordenada por 2 botones pulsadores, además que cuente con interruptores de límite en ambos sentidos, que los movimientos sean determinados por el giro de un motor eléctrico y cuando dejemos de presionar los pulsadores la mesa pare.

Aquí planteamos que tenemos cuatro  variables de entrada y dos de salida.

Planteamiento de mesa transportadora

Análisis  Lógico

Una tabla de verdad nos permite analizar las posibilidades lógicas reales, por ejemplo nuestra mesa no se pude mover en ambos sentidos al mismo tiempo.

Análisis lógico de la mesa transportadora

3.- Simplificación de ecuaciones.

Es aquí donde tiene lugar la aplicación del álgebra de Booleana (creada por Gorge Boole).

Aplicación del algebra Booleana para mesa transportadora

4.  Implementación del circuito lógico de control.

De las ecuaciones lógicas simplificadas obtenemos el circuito lógico más simple.

Implementación del circuito lógico de mesa transportadora

Este circuito de control es la base de nuestro circuito final, “MD” y “MI” son las bobinas de los contactores que ordenaran el cierre de contactos en el circuito de potencia que determinan el giro del Motor eléctrico.

También nos faltarían los elementos de protección contra cortocircuitos y sobrecarga.

Identidades lógicas

Las identidades lógicas son  pequeñas igualdades que realizan idéntica función.

Su empleo tiene lugar en la simplificación de ecuaciones lógicas utilizando el “Álgebra de Boole”.

La simplificación busca obtener un circuito lógico con menos componentes.

·       Identidades básicas

1.- Un mismo botón  conectado 2 veces normalmente abierto. 

Identidades básicas  botón  “a” doble  N.A.

2.- Un mismo botón  conectado normalmente abierto  y normalmente cerrado.

Identidades básicas  botón  “a” doble  N.A. y N. C.

S= 1 representa un interruptor permanentemente cerrado (como corto circuito sin control) y S = 0 un interruptor permanentemente abierto (como un circuito abierto)

3.- Un botón  conectado en función “O” Interruptor con un 1 ó con un 0 lógico. 

Identidades básicas   función “O”  Interruptor con un  1 ó con un 0 lógico.

4.- Un botón  conectado en función “Y” Interruptor con un 1 ó con un 0 lógico. 

Identidades básicas   función “Y” Interruptor con un 1 ó con un 0 lógico. 

El siguiente ejemplo ilustra la aplicación de las identidades lógicas.

Álgebra de Boole

Circuitos equivalentes lógicos 

Lógico el de menos elementos es más económico y de menor mantenimiento.